What is Pythagoras’ Theorem?

Pythagoras’ Theorem is one of the most fundamental principles in mathematics, particularly in geometry. It states that:

In a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.

Mathematically, this is written as:

a² + b² = c²

Where:

• a and b are the lengths of the two shorter sides,
• c is the length of the hypotenuse (the side opposite the right angle).

This formula appears in nearly every GCSE Maths syllabus and is a cornerstone of the geometry section.

A Quick Look at Pythagoras

Pythagoras was an ancient Greek philosopher and mathematician born around 570 BC. He founded a religious movement known as Pythagoreanism and is credited with the discovery of this famous theorem. How to Teach Punctuation to Primary School Children

Although some historians debate whether he discovered the formula himself, it’s undeniably named after him due to his immense influence on mathematical thought.

Definition of Pythagoras’ Theorem

Let’s break down the formal definition in a simpler way:

• A triangle must be right-angled.
• The longest side is always called the hypotenuse.
• If the other two sides are a and b, then:
  a2+b2=c2a^2 + b^2 = c^2a2+b2=c2

This relationship allows you to find a missing side if you know the other two. GCSE English Literature Guide

Understanding Right-Angled Triangles

Before applying the theorem, you must correctly identify the triangle’s parts.

Key Properties

• One angle = 90°
• The side opposite the right angle = hypotenuse
• Remaining sides = legs

Labelling the Triangle

When solving problems:

• Label the hypotenuse as c
• Other sides as a and b

Always identify the hypotenuse first.

Step-by-Step Breakdown of the Theorem

Step 1: Identify the triangle

Check that one angle is 90°. No right angle? No Pythagoras.

Step 2: Label sides

Use a, b, and c as per the rules.

Step 3: Substitute values

Plug known values into the formula.

Example:

If a = 3 cm, b = 4 cm:

c2=32+42=9+16=25⇒c=5 cmc^2 = 3^2 + 4^2 = 9 + 16 = 25 \Rightarrow c = 5 \text{ cm}c2=32+42=9+16=25⇒c=5 cm

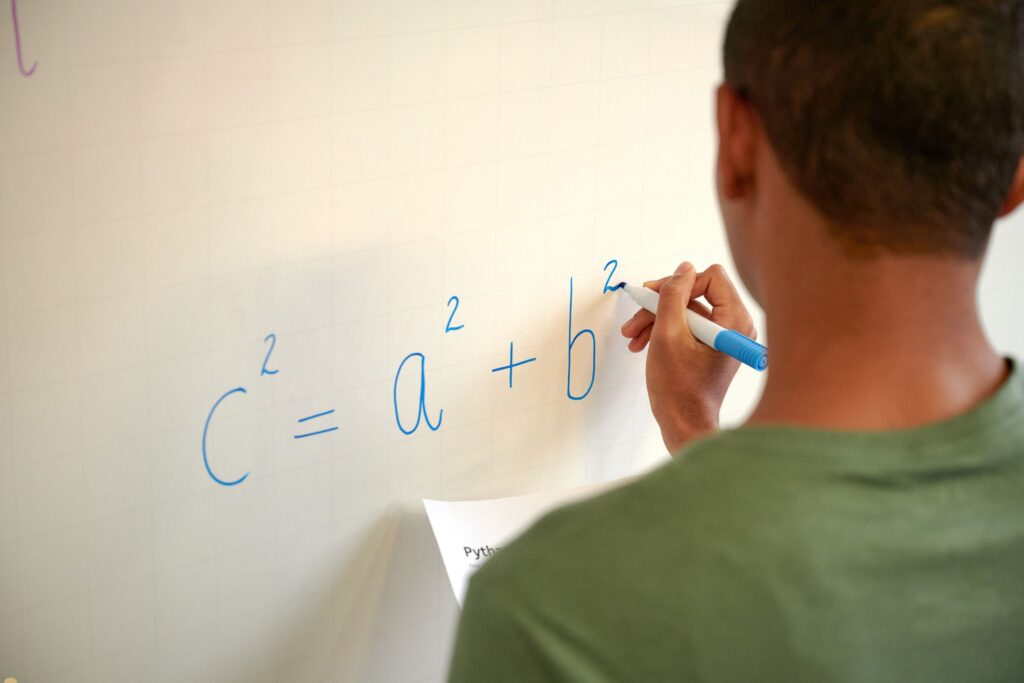
Formula in Practice

Here’s how this formula applies to real-world tasks:

Scenario	Description	Use of Theorem
Measuring ladders	Finding how far a ladder reaches a wall	a² + b² = c²
Mapping	Shortest distance between two points	Ideal for GPS and route planning
Construction	Calculating material lengths	Useful in roofing, walls, beams

When Can You Use the Theorem?

You Can Use It When:

• You know two sides of a right-angled triangle
• You want to find the third side
• The triangle is 2D

You Can’t Use It When:

• The triangle doesn’t include a right angle
• You’re missing two side lengths
• You’re working with non-Euclidean geometry

Common Misconceptions

1. Mixing up sides – Always identify the hypotenuse properly.
2. Applying it to non-right triangles – It simply doesn’t work.
3. Forgetting to square root – After a² + b² = c², don’t forget to find c by square-rooting.
4. Using it in 3D without modification – 3D problems need special handling.

Real-Life Uses of Pythagoras’ Theorem

Believe it or not, Pythagoras’ Theorem is used daily in several professions.

Fields Where It’s Used:

• Construction: To ensure walls are straight.
• Architecture: Designing ramps and slopes.
• Navigation: Air and sea travel routes.
• Technology: In computer graphics and simulations.

Pythagoras vs Trigonometry

Feature	Pythagoras	Trigonometry
Uses	Side lengths	Angles & sides
Needs right angle?	Yes	Yes
Formula type	a² + b² = c²	sin, cos, tan
Best for	Finding sides	Finding angles

Exam Tips & Tricks

• Always label your triangle clearly.
• Double-check for a right angle.
• Write units in answers.
• Use a calculator wisely – round only at the end.
• Memorise the formula but understand how to use it too.

Practice Problems (With Answers)

Question	Answer
1. a = 5, b = 12. Find c.	13
2. a = 6, c = 10. Find b.	8
3. b = 7, c = 25. Find a.	24
4. a = 9, b = 12. Find c.	15
5. a = 1, b = 1. Find c.	1.41 (rounded)
6. Is a triangle with sides 5, 12, 13 a right triangle?	Yes
7. Is a triangle with sides 2, 3, 4 a right triangle?	No
8. Find the diagonal of a 6m by 8m rectangle.	10m
9. A 5m rope supports a pole and stands 4m tall. Distance from base?	3m
10. Find c if a = √2, b = √2.	2

Conclusion

Pythagoras’ Theorem is more than just a formula; it’s a tool that applies in real life and exams alike. You’ll build strong foundations in geometry by understanding its logic, labelling correctly, and practising problems. Enrol for Online Tutoring UK

FAQs

1. Can I use Pythagoras’ Theorem on any triangle?

No, only right-angled triangles.

2. What’s the hypotenuse?

The side opposite the right angle and always the longest.

3. Do I need to learn this by heart?

Yes, especially for non-calculator papers.

4. How is it tested in GCSE exams?

Usually through missing side questions, word problems, or multi-step geometry.

5. Can it be used in coordinate geometry?

Yes, particularly for finding distances between points.